The Power of Exponential Growth

Chapter 2 additional material

Unit Organization:

• Exponential Growth
• Population Growth
• Carrying Capacity and Overpopulation
• Malthus and the Demographic Transition
• Population Policy
• Ancillary Resources and Links

Source:

The source for this material is a lecture posted by Dr. Albert Bartlett, then an emeritus professor of physics at the Universithy of Colorado, on youtube.  You can watch the original there.  In addition, if you google him, you can find this topic discussed by him in several publications on the web.

Exponential growth

• Exponential growth is growth by a constant % in any given time span (often years for human data)
• Another way to look at this same phenomenon is to ask, how long would it take for something (human population size, consumption of electricity or macadamia nuts) to increase by a constant fraction
  • these fractions are not limited - can be 5%, 50%, or 500%
  • the most commonly used fraction is 100%, which is the time it takes something growing at a constant rate to double in size.
• Calculation of the time it takes to grow by some amount for something growing at a constant rate (we will express this rate as a % in this tutoril) is simple to do, expecially for fractions that represent integer increases (doubling time is 2x, tripling time is 3x, and so on).
  • Take the natural logarithm of the integer (or the number if, for some reason, you wanted the time it would take to grow 2.5x or some other non-integer) and multiply it by 100 (needed to keep the units equivalent because we are using rates that are percents, which is a fraction multiplied by 100)
    • For 2x, the natural log = ln(2) = .693 x 100 = 69.3, which is very close to 70, an easier number to remember
  • Divide 70 by the rate of growth (expressed as a percent) and you get the doubling time:

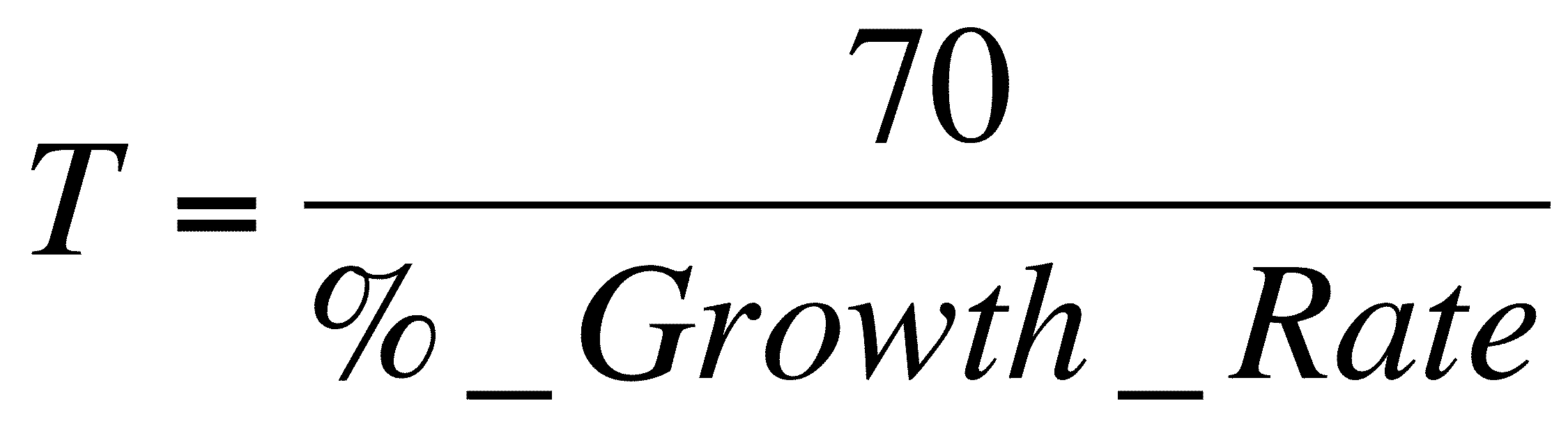
• The units of T are the same as the units in the rate (often, but not always years for the date we will deal with in this course)
• The doubling time for a population growing at 7% a year is just 10 years (14 years for 5% a year growth, 35 years for 2% growth, etc.)
• To see if you get the idea, try to calculate the tripling time for something growing at 5% per year (round the numerator of the equation to the closest integer)
  • The answer is 22 years and you should be able to calculate it (and you now can calculate the tripling time for any constant % growth rate) and, if you push it to a quadrupling time for 5% growth, its about 28 years
  • Notice that the times are getting closer together.  Why is that? 

Importance of Exponential Growth

Future of Human Population

• Recent decline in growth rate
• Predictions of growth generally reflect the recent decline and show a slowing of growth
  • Most show us reaching at least 9,000,000,000 from the current 7,000,.000,000 by 2050 but that the time to add additional billions will be increasing (not decreasing as it has been)
• Predictions beyond 2050 reflect outlook of those doing the prediction
  • Some will show a "maximum" population, others will assume no limit

Understanding Doubling Times

The outcome of exponential growth is hard for most of us to really understand, at a gut level

Doubling times give us a way to put the outcome steady growth into terms we can understand

To do this, lets try to work out the implications of doubling time with an example.  Bartlett has in interesting one, and I will use it here (slightly modified)

• You win a game of chess and you opponent is Bill Gates.  What have you won?  He gives you two options.
  1. Half of his money.
  2. If you place a dollar on the first square of the chess board, he will double it on the second square, then double the money that's on the second square on the third square, double the third square on the fourth, and so on.
• Which would you choose?  The first option gives you over $20,000,000,000 but the second option is better!

• By the 20th square, you have become a millionaire but not a billionaire yet. When you reach the 40th square, however, you are the world's first trillionaire and by the 64th square you are a quintillionaire and your wealth ceases to have any real meaning: you can buy everything anyone has for sale for many centuries (the numbers for the 64th square are approximate because of the limits of my computer).
• Conclusion 1:  exponential growth produces outlandish numbers if unchecked
  • This might not be so unexpected if you have ever dealt with exponential growth but it is a point worth re-emphasizing
• Conclusion 2:  Every doubling time produces more (or uses more, if this is a model of consumption) than All OF THE PRECEEDING DOUBLINGS ADDED TOGETHER
  • This is not something most people understand and it is, when applied to the real world, almost not believable. 
  • Since we started to use oil in the US, the growth rate of oil production (and consumption, as we use almost everything we produce) has been about 7% per year, which leads to a  doubling time of 10 years.
    • In 1977, then President Jimmy Carter told the American public in a televised speech on energy:

    "The world has not prepared for the future. During the 1950s, people used twice as much oil as during the 1940s. During the 1960s, we used twice as much as during the 1950s. And in each of those decades, more oil was consumed than in all of mankind's previous history."

  • Many simply couldn't believe it but believe it, it's true.  We will look closer into the supply of energy later but I want to emphasize here that one must think in exponenetial terms, not arithmetic terms, when approaching such topics as population growth, production, and consumption.

How long before it's all gone??

How much will things change in your lifetime?

• Let's assume you will live 70 years (look at the equation above for why this number was chosen)
  • If you live that long, the rate of growth will tell you how many times things will multiply in your lifetime
  • Simply take the rate of growth (expressed as a percent) and raise 2 to that number
• 1% is 2 to the first power, or 2 : things will double in your lifetime
• If they grow be 4%, then the factor is 2 to the 4th (4 twos multiplied together), or 16 : things will grow by a factor of 16 in your lifetime.  Think of a steady rate of inflation.  Then the average price of things will go up by a factor of 16 in your lifetime at 4% inflation.
  • Think about 8% inflation (which we have seen in the US for brief periods).  If it persisted for 70 years, things would go up by a factor of 256.  Ten dollars of groceries at your birth cost 2,560 dollars at your death.

Growth on a finite resource (or planet)

Imagine you are a bacterium.

In the growth medium you prefer, you can divide every minute (i.e., you double every minute)

One of you is placed in a liter flask of medium at 11 AM

At 12 noon, the bottle is full and growth stops

Let's look at the implications of this situation

• When was the bottle half full?
• The answer is obvious, it was 11:59, one minute before it was full
• Let's look into the past, to see our situation minute by minute

  Time	Fraction of total	% Used	% Remaining
  11:51	1/512	0.2%	99.8%
  11:52	1/256	0.39%	99.6%
  11:53	1/128	0.78%	99.8%
  11:54	1/64	1.56%	98.4%
  11:55	1/32	3.13%	96.9%
  11:56	1/16	6.25%	93.7%
  11:57	1/8	12.5%	87.5%
  11:58	1/4	25%	75%
  11:59	1/2	50%	50%
  12:00	1	100%	0%

• Look at the last column.  When would you start to worry about what is left.  Remember that you had been in the flask since 11:00, and at 11:55, things look great as you still have 97% of your resource left.
• You are five minutes from doom.
• Well at 11:59, you see your peril and, in a remarkable accomplishment for a bacterium, you send out explorers to find new resources.  Hooray!! They are successful and find 3 more liters of growth medium
• This is like the recent discovery of vast "shale gas" reserves.
• Now, how long will it take to reach doom now that you 4 times your original amount of resource?
• Doom at 12:02
• When you hear about huge new discoveries of oil, gas, coal, or minerals, evaluate the discoveries in the light two scenarios:  steady growth (the accepted model of consumption) vs steady-state (stable) consumption

Expiration Time - This section and the rest of this page are still in development!

The problem:  How long will it take to use up a known resource when consumption of that resource is growing steadily (at a constant percent)

• Approach depends on whether or not you assume a carrying capacity and how close you think we are to reaching that number

If there is a population problem:

Many policy approaches are possibleXXXXXX

An

• Ma)
• b₀  r²
  .

Last updated September 1, 2012