Introduction to Comparing Many Means

Chapter 11, part B

Email me

Back to:

This is the Second part of a two-part set of lecture notes. The First part can be found here

Unit Organization

• Two-Way ANOVA - Factorial Designs
  • Two-Way Factorial analysis
  • Calculating and analyzing the two-way ANOVA
• Linear Combinations
• Multiple Comparisons
  • Bonferroni Adjustment

Problems:

Problems for homework

• 3rd Edition - 11.17, 11.18, 11.22, 11.24, 11.25, 11.26, 11.33, 11.34, 11.38, 11.44
• 4th edition - 11.7.1, 11.7.2, 11.7.6, 11.8.2, 11.8.3, 11.8.4, 11.9.1, 11.9.2, 11.9.6, 11.S.5

Problems for homework

• 3rd Edition - Do at least 1 additional problem in each section covered by this lecture
• 4th edition - Do at least 1 additional problem in each section covered by this lecture

Two Way ANOVA - Factorial Designs

Before we go any further into two-way ANOVA, we should consider a complication not covered in your textbook

There are two models for ANOVA, whether ANOVA or MANOVA

These models differ in their original assumptions, but the calculations and analyses done here are not affected by the difference between the models (so this is being added for future reference only)

The models differ in the assumptions about what the treatment levels represent.

Fixed-Effects Model

In this model, the treatment levels represent fixed classes.

The classes are determined by the experimenter and it is these classes about which the experimenter wished to draw conclusions, not about all possible classes.

Examples

The experimenter uses classes that cover all possibilities (two sexes, all possible genotypes at a locus, etc.).

Suppose there are two known populations of a species of mammal - one each from two different islands. and the experimenter has a treatment called Variety with two levels - one from each island.

The effects are fixed because there are no other populations to consider, differences between these two locations are the differences due to geography in this species (compare this to the example below under random-effects model).

Random-Effects Model

Here, the classes arde not determined fully by the experimenter.

The differences among the treatment levels are meant to be a sample from a wider universe of possible treatment levels, randomly chosen (a quality not often achieved).

Examples

The experimenter has collected bacteria from the same species from around the world. He sets up an experiment in which strains from 5 of the many locales become treatment levels.

The conclusions here will be about geographic differences among the strains in general, not just between the 5 locales represented in the experiment.

The SS, MS and ANOVA tables almost always look the same for these two models.

The differences come in how some hypotheses are tested (which MS terms are used for the F-test) and how some secondary analyses, such as multiple comparisons, are made.

Mixed-Effects Model

This is simple a MANOVA in which some treatments are fixed-effect and some are random-effect

The fixed-effect model is the one presented here and applies to almost all examples in the book. Random- and Mixed-effect models will have to await another course.

Two-Way Factorial analysis

Factorial comes from calling a treatment a FACTOR and the treatment groups LEVELS of that factor. It's just a change of name.

This design is similar to the two-way ANOVA in which one of the treatments is blocks, which we treated above.

We will only consider a limited set of factorial designs

Those in which all combinations of factor levels are present (called a complete factorial design), for example:

If we have 2 sexes and 3 drug levels, then there are 6 combinations (three drug levels in each sex).

If we have 3 sexes (possible in some species) and 3 drug levels, then there are nine combinations.

Each combination of treatments must then be done more than once (= must be replicated) and usually is done three or more times.

So, if we have two sexes, three drug levels, and five replicates, then we have a total of 30 (= 2 * 3 * 5) observations.

Adding one level to the first factor increases the number of observations to 45 (= 3 * 3 * 5).

Adding one level to the second factor increases the observations to 40 (= 2 * 4 * 5).

How does a factorial design differ from the blocks design above?

In the blocks design, we were really only interested in the treatment effects, not the block effect, so some of the potential analysis was simply ignored.

Now lets use an example to see what sorts of analyses can be done when we are interested in both of the treatments (= both of the factors)

We will use a very simple example in which there are two factors, each with two levels.

An experiment is done to understand how genotype and environment affect the size of adult flour beetles. The environmental difference lies in the moistness of the flour the beetles inhabit, so we have high and low moisture levels of this factor. The genetic factor compares two inbred lines of beetles collected in locales that were far from one another: the Atlanta genotype and the Brisbane genotype. The beetles were all reared from eggs in bottles of flour (each bottle had one genotype of beetle and either high or low moisture) and the average size of the adult beetles is an observation (so this is a population level study - the experimental units are the populations in the bottles).

Before we go farther, lets consider some of the many possible outcomes for this experiment. The ones we will consider are graphed below.

First chart

Both genotypes appear to grow better when in the low-moisture flour.

Second chart

Both genotypes appear go grow better in the low-moisture flour.

The Atlanta genotype appears to really like the low moisture, the effect is less pronounced for the Brisbane genotype.

Third chart

The Atlanta genotype grow better in the high-moisture flour.

The Brisbane genotype grows better in the low-moisture flour.

These three charts represent are very different outcomes.

Can one analysis give us the statistical power to test all of them? ANOVA can.

Lets consider the first chart again and make some true statements about the outcomes.

The Brisbane and Atlanta lines produced different sizes of adults, so there was an effect of the genotype factor.

The High and Low Moisture lines produced different sizes of adults, so there was an effect of the moisture factor.

The effect of moisture on the Atlanta line was the same as it was in the Brisbane line.

This last true statement can also be restated in terms of the independence of the two factors:

Both factors had independent effects on the size of adult beetles.

When factors have independent effects on the response variable, the factors are also said not to INTERACT.

Lets consider the second chart again and make some true statements about the outcomes there.

The Brisbane and Atlanta genotypes produced different sizes of adults, so there was an effect of the genotype factor.

The High and Low Moisture treatments produced different sizes of adults, so there was an effect of the moisture factor.

The effect of moisture on the Atlanta genotype was more pronounced than on the Brisbane line.

These two factors are not independent here, they interact.

The third case is also a case of interaction.

Here the interaction is so pronounced that the trends within lines (with respect to the effect of moisture) are opposite of one another.

Calculating and analyzing the two-way ANOVA

So, how do we test these null hypotheses? -

H₀: There is no effect of genotype.

H₀: There is no effect of moisture.

H₀: There is no interaction between genotype and moisture (interactions are often symbolized like "genotype x moisture").

To do this, we will need to add SS_{(interaction)} to our table and then use the appropriate MS ratios to do an F-test for each of the null hypotheses.

Remember, from the section on blocking in the previous lecture, that the sum of squares for the treatments are as follows (n is the number of observations in the ith level of treatment A and mi is the number of observations in the j treatment of treatment B):

Treatment A in our present example would be  Genotype and treatment B would be Moisture and I and b are the number of levels of treatment A and B, respectively

We need to define the SS_{(interaction)}, SS_(within) and SS_(total) so that we can incorporate them into our calculations.

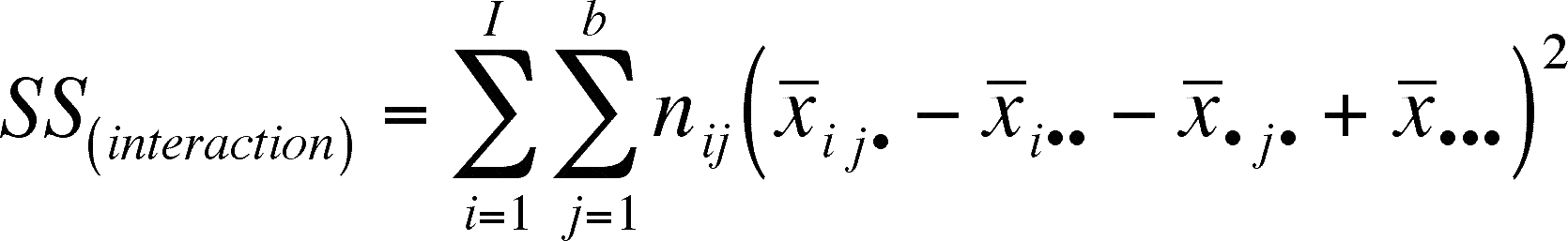
note that we want to preserve as many of the previously used symbols as possible so, I is the number of levels of treatment A, b = number of treatment levels for factor B and n_ij = number of replicates within each combination of factor A and B (they may differ, so we need to index them).

In English, the interaction terms that are added are the squares of the mean of each combination of treatments minus the mean for treatment A, minus the treatment B mean, plus the overall mean.

SS_(error) is found by subtracting from each observation the mean of the treatment combination to which the observation belongs.

SS_(total) is found in the original way - simply subtract the overall mean from each observation, square the difference, and sum the squares.

In this case, the SS_(total) is being partitioned into four terms:

SS_(total) = SS_{(Factor 1)} + SS_{(Factor 2)} + SS_{(Interaction)} + SS_(error)

Since SS_(treatments) is calculated in the same fashion, all of the SS_(blocks) are being taken from SS_(error) (SS_(total) will not change).

The model we will use is this:

Any observation, x_ijkl, is the sum of four things: the overall mean, the effect of first factor level i, the effect of second factor level j, the effect of the interaction (k), and the effect of random error within first factor i and second block j (the random error term is again the within-cell variation).

If we let tau () symbolize the first factor's effect, = the second factor's effect, = the interaction effect, and epsilon () = the random error, then

x_ijk = + _i + _j + _k + _ijk

or, if we use our estimates of these population values

x_ijk = x_••• + (x_i•• - x_•••) + (x_•j• - x_•••) + (x_ij• - x_i•• - x_•j• + x_•••) + (x_ijk - x_ij•)

With this model, the null hypothesis is that all of the values are equal to 0, so that there is no effect of belonging to a group. The second null hypothesis is that all of the values are equal to 0, and the interaction null hypothesis is that the values are all 0.

Since the total SS_(total) is fixed and the SS_{(Factor A)} and SS_{(Factor B)} are not changed, what the model above does is remove more of the SS_(error) , with the expected effects on the MS term and all ratios in which it appears.

The table for this is below (the MS terms = SS divided by the df, as before):

Source	d f	SS	MS
Factor A	I -1	SS(Factor A)	MS(Factor A)
Factor B	b - 1	SS(Factor B)	MS(Factor B)
Interaction	(I - 1) * (b - 1)	SS(Interaction)	MS(Interaction)
Error	n* - (I * b)	SS(error)	MS(error)
Total	n* - 1	SS(total)

F-value for the Factors A and B are MS_(Factor) divided by MS_(error), with appropriate numerator and denominator df.

F-value for the Interaction is MS_{(Interaction)} divided by MS_(error), with appropriate numerator and denominator df.

The book recommends a step-by-step analysis of such a table.

First, determine if the null hypothesis of no interaction with the interaction F-value.

If the null is accepted, then

Test for Factor A effect with the appropriate ratio and test for Factor B effect with the appropriate ratio.

If the null is rejected,

Consider the two factors as separate experiments and analyze each separately with the appropriate tests

t-tests here, since there are two levels of each factor

Use a one-way AN OVA for any factor with more than two levels.

A question: Where did the control treatment go?

Linear Combinations (Contrasts)

If you want to adjust a factor's level's effects according to some scheme, you can make linear combinations of the level's means. Suppose factor A has i levels, then:

L = m₁x_1• + m₂x_2• + m₃x_3• + m₄x_4• + ... + m_ix_i•

The m terms (unfortunate choice since m has already been used in this chapter) do not all have to be the same.

They could be some importance factor you have assigned.

L would be the overall effect adjusted for the importance of each level.

They could reflect some aspect of the population (the book uses their prevalence in the population as an example).

L would be the overall effect adjusted for the prevalence of each level in the population (see book example).

What if you want to know if certain of the treatment levels are different from other levels? This might be the case if you have several levels and only the last two (or last one) look like they are very important, of if you want to group the levels by how large their effect was.

This can be done with linear combinations in which the m's add to 0.

First you have to construct a linear combination that satisfies the contrast requirement. Suppose there are five levels and you want to:

Compare the first three to the last two (to see if the two groups of levels represent two different magnitude of effects)

L = 2x_1• + 2x_2• + 2x_3• - 3x_4• - 3x_5•

Compare the first and last effects

L = 1x_1• + 0x_2• + 0x_3• + 0x_4• - 1x_5•

In the first case, 2 + 2 + 2 - 3 - 3 = 0 and in the second, 1 + 0 + 0 + 0 - 1 = 0.

The significance of the contrast can be tested with either a t-test or a confidence interval.

A linear contrast is the estimated effect of those factors (scaled by the m's) and if there was no difference, then L is 0 and what we measured in the experiment is due to random error, so

H₀: L = 0

Nondirectional alternative

Assuming that an -level has been chosen, one can calculate either the confidence interval for L (to see if it includes 0) or just do a standard t-test.

To do the t-test or CI, we need a standard error of L, which is:

The pooled variance (s²) is simply the MS_error. The df = df_error.

CI = L ± t_{alpha, df} * SE_L

or

t_s = L / SE_L, df = error df

If you accept the null, then the overall effect (L) is not different from 0, which means no effect.

If you reject the null, the alternative is that L is nonzero.

Multiple Comparisons

What if you don't have any interest in a particular level but you want to test all pairwise comparisons between levels within a factor?

Pairwise t-tests with individual contrasts would mean lots of t-tests, which increases the chance of a type I error.

In the example from the above, five levels would mean 10 (= 5!/(2!3!)) different t-tests.

The way to reduce the risk of type I error is to use one of the several ways of controlling it by adjusting

Student-Neuman-Keuls Test

This test is useful only if all of the n_i's are the same.

You need all of the treatment level means, arranged from smallest to largest.

Calculate the scale factor as: , where s²_(error) = MS_(error). Remember, error SS is the same thing as within SS.

Table 11 in the book has the q_i (constants you will need). There are tables for only two -levels, 0.05 and 0.01. The df to use is the df from the SS_(error) (see the appropriate ANOVA table).

You will notice that there are 9 columns (from 2 to 10). The values in each column are used to calculate R_i's:

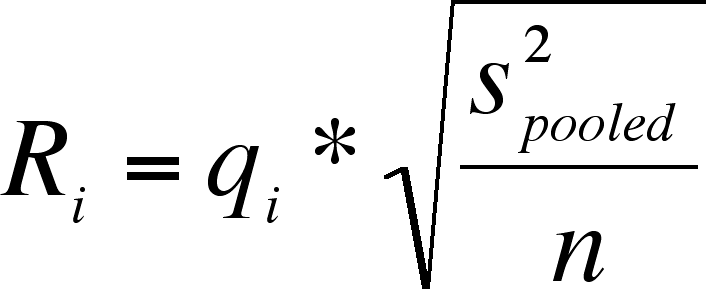
Only calculate I - 1 of these (I = number of treatment levels)

Now arrange the R_i's from smallest to largest.

Calculate the difference between the largest and smallest means.

If the largest R_i is larger than the difference, then there is no difference between the largest and smallest means and you will accept all null hypotheses. Draw a line below all means and end the procedure

If the largest Ri is smaller than the difference, then the largest and smallest means differ significantly and so you proceed to the next comparison.

Reduce the number of means considered by 1. There are two ways to do this.

Eliminate the largest mean.

Calculate the difference between the second largest mean and the smallest.

Compare the difference to the second largest R_i.

If the second R_i is larger than the difference, then there is no difference between these means. Draw a line below these means.

If the second R_i is smaller than the difference, then the second largest and smallest means differ significantly.

Eliminate the smallest mean.

Calculate the difference between the second smallest mean and the largest.

Compare the difference to the second largest R_i.

If this R_i is larger than the difference, then there is no difference between these means. Draw a line below these means.

If this R_i is smaller than the difference, then the second smallest and largest means differ significantly.

If you have not drawn lines for both of these comparisons, go on.

Reduce the number of means considered by 2. There are three ways to do this.

Eliminate the largest and second largest mean.

Eliminate the smallest and second smallest mean.

Eliminate the smallest and the largest mean.

For each of these eliminations, calculate the difference between the largest and smallest mean remaining

Compare the difference to the third largest Ri and draw a line under the means or not as above.

If you have not drawn lines for all of these comparisons, go on.

When doing this, there is no need to look in any sub-group that has already been underlined. The underline means all means have already been shown to be the same.

Reduce the number of means considered by 3. There are four ways to do this The number of ways is always the number of means eliminated +1).

Proceed as above for any sub-groups that have not already been underlined.

Continue eliminations until all but 2 means have been eliminated or until there are no more subgroups not underlined already.

Those means that are underlined are not different at the chosen -level. Those not connected by the same underline are different.

Bonferroni Adjustment

An alternative is to do all of the t-tests, but to adjust the -level so that the overall risk of a type I error is below the original -level.

Calculate the number of t-tests you will do.

Divide the -level by this total and use the resulting fraction as your -level for each individual test.

Note that you can use this adjustment for any repeated set of statistical tests.

If you are doing a series of tests, you can adjust the -level for each individual test in the same way.

One may also use this adjustment for Confidence Intervals by adjusting the individual -levels before looking up the t-values to be used.

Last updated October 27, 2011