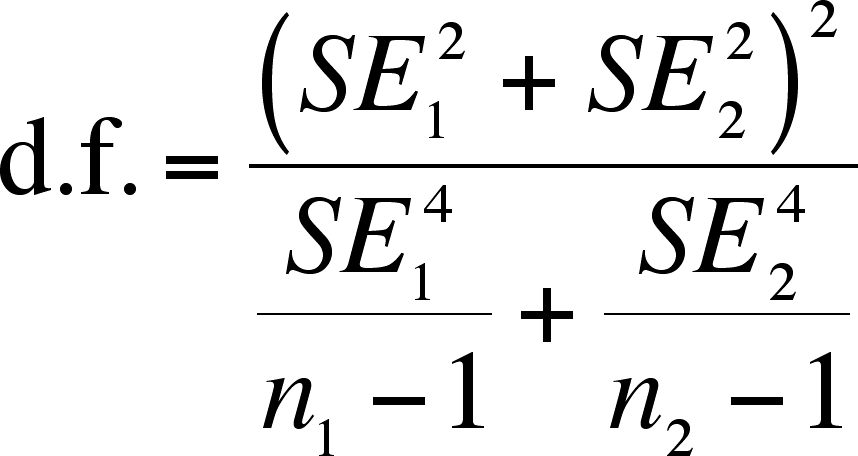|
BIOL 3110
Biostatistics
Phil Ganter
320 Harned Hall
963-5782 |
Confidence Intervals
Chapter
6 (4th edition)
or Chapter 6 (3rd edition,except
sections on proportions) and part of Chapter 7
(3rd edition,
first sections on confidence interval of the difference between means)
Email me
Back to:
Unit Organization:
Problems:
Problems for homework
- 3rd edition:
6.3, 6.7, 6.10,
6.25,
6.29,
6.32,
6.34, 7.4, 7.5,
7.19, 6.52,
6.58
- 4th edition:
6.2.3, 6.2.7, 6.3.3, 6.3.19, 6.4.4, 6.5.2, 6.5.4, 6.6.3, 6.6.4, 6.7.11, 6.S.2,
6.S.8
Suggested Problems
- 6.1,
6.2, 6.12, 6.14, 6.16, 6.18, 6.27, 6.31, 6.39, 6.43, 7.1, 7.2, 7.11,
7.17, 7.18, any from the section of problems at the chapter's end
- 4th edition:
6.2.1, 6.2.2, 6.3.5, 6.3.8, 6.3.10, 6.3.12, 6.4.1, 6.5.1, 6.6.1,
6.6.2, 6.7.2, 6.7.9, 6.7.10, any
from the section of problems at the chapter's end
Statistical Estimation
This is the reason for doing
statistics in the first place.
Statistical estimation has two
components
- estimation
of some population parameter (mean, st. dev., shape of the distribution, etc.)
- determination
of the precision of the estimate (how likely is it to be correct?)
In this lecture, we will learn how
to construct confidence intervals, which depend on us knowing two
things:
- an
estimate of the true mean
- an
estimate of the spread of the data about the true mean
As discussed before, the best
estimate of the true mean is a sample mean (or, better, a mean of
sample means)
this leaves us with the problem
of estimating the true standard deviation (it's not exactly
s)
Standard Error of the mean
- First, let's recall what the
standard deviation is:
- a
measure of the dispersion (=spread) of the data around the mean, variation
causes the data points to differ, not error
- when
there are lots of big and small values but few in the middle, the st .dev.
is larger than when most of the data is near the mean
- The
standard deviation of sample means is
caused by sampling and measurement ERROR, not variation (by our definitions)
and so should really be called "error" not "deviation" but we will follow
standard usage
- The
standard deviation of sample means is likely to
be smaller than the standard deviation estimated
from
a single sample or the true population standard deviation
- When
means are calculated from samples drawn randomly from a population, they will
most often be closer to the true mean than will a single data point drawn
from the population at random
- Thus,
a standard deviation calculated from 10 means will be smaller than a standard
deviation calculated from 10 values drawn at random from the population
- Thus, to
calculate the standard error of means, we need a formulation that will
guarantee that it is smaller than the population standard deviation (
 )
)
- There
is a second consideration and that is that samples are not all equally good
- Means
calculated from large samples are more likely to be nearer the true
mean
(
 ) than those calculated from small samples.
) than those calculated from small samples.
- If
this is so, then a standard deviation calculated from small sample means
(which are clustered less tightly about the true mean) should be larger
than a standard deviation calculated from large means (which are clustered
more tightly about the true mean)
- So,
taking both considerations into effect, we use this equation:
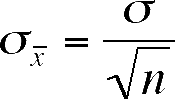
- Note
that we use the square root of the sample size (remember that
 is a square root also)
is a square root also)
- A practical problem is embedded in the above definition
of the standard error of sample means.
- To calculate the standard
deviation of the means, we needed the standard deviation of
the population
- This
is not usually something we know, so we need a fix, a way to estimate
this from a single sample
- So, what can we use to estimate sigma, (
 )?
)?
- If we get something to estimate sigma with that
we can actually measure, then we can use it to find the probability of a sample
mean being close to the actual mean (
 )
)
- The most obvious estimate, and the one we will
use is s, the standard deviation of the sample, which we
will substitute into the formula for the standard deviation of the sample
means
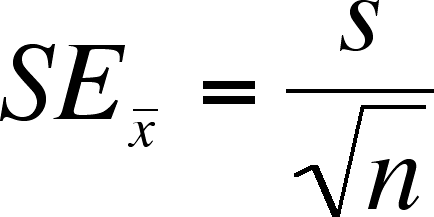
- We
call the standard error (SE) of the mean, not the standard deviation
of the mean because it is a measure of the error in the sample mean,
not a measure of the variation among data points.
Difference
between SE and SD
- Standard
deviation of the sample - refers to how the individual data
points are distributed with respect to the mean, it is a
measure of data dispersion.
- Remember how it is computed (as the square
root of the average [corrected for degrees of freedom] of the squared deviations
of the data points from the mean [remember we square as a means of making
all of the deviations positive])
- Standard Error of the mean
- refers to the probability that sample means, not individual data points,
differ from the true population mean
- The book states the same thing with different
words. The book defines the SE as a measure of uncertainty due to sampling (random) error in how good a sample
mean is as a measure of the true mean
- A larger SE means there is more uncertainty
in using the sample mean as an estimator of the true (population) mean
- Remember that SE is related to s, but that
it is always smaller than s
- The divisor means that larger samples
have a smaller SE, that is, that they are expected to be closer to the
true mean than are sample means from smaller samples
Confidence Interval for the True
Mean
A confidence interval is a range of
values between which we believe the value of interest to lie
- for us
 , the mean of the population, is the
value of interest
, the mean of the population, is the
value of interest
The size of the range depends on
two things
- how
sure (confident) we want to be
- if we want to me more sure,
then we must have a larger range
- you can be somewhat
sure that the true mean of the student age at TSU is
between 20 and 30
- you can be totally sure
that the true mean of the student age at TSU is
between 1 and 100
- how
much random variation there is the original population
- If we knew
 ,
the population standard error, we could get the range for
,
the population standard error, we could get the range for  , the sample mean, given that
the population is normally distributed
, the sample mean, given that
the population is normally distributed
- if you want to know how
big a confidence interval you need to be 75% sure
that the mean is in the value you have to find the z
values that have 75% of the area under the normal
curve between them (see below, to see that these
values are about -1.03 and 1.03)
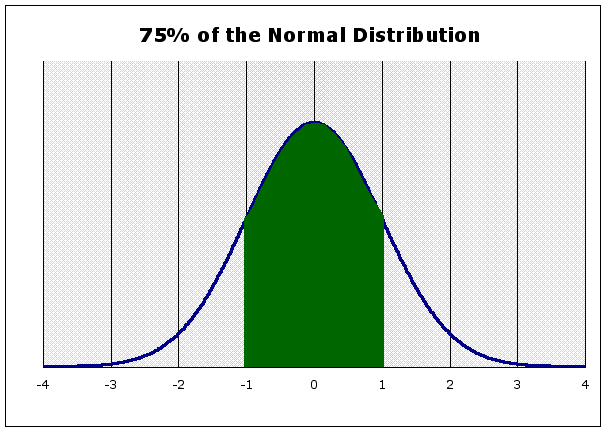
Then one would find X,
the actual numbers, from the z values (remember how
you calculate a z) as done below
The
confidence interval when sigma is known:
Start with the proposition that the
probability of Z being between -1.03 and 1.03 is 75%
Pr{
-1.03 < Z < 1.03} =
0.75
Substitute the formula for calculating Z based on
the sample mean (because it has  and
and  in it, and we want to know how one relates to the other)
in it, and we want to know how one relates to the other)
Pr{-1.03 < 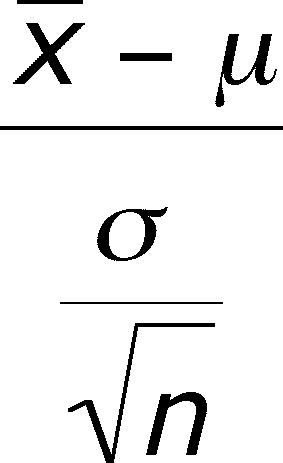 < 1.03} = 0.75
< 1.03} = 0.75
Now do some simple algebra to find out where  should lie
should lie
- first, multiply by the denominator,
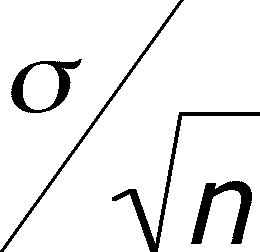 , to eliminate it from the middle term and then subtract
, to eliminate it from the middle term and then subtract  to remove it from the middle term, last multiply
by -1 )
to remove it from the middle term, last multiply
by -1 )
- Pr{-1.03*
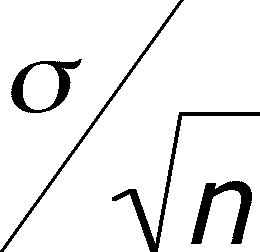 <
<  -
-  < 1.03*
< 1.03*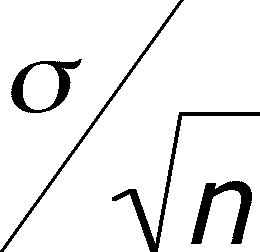 } = 0.75
} = 0.75
- subtract
 from all 3 terms and then multiply
by -1 to turn a negative
from all 3 terms and then multiply
by -1 to turn a negative  into a positive
into a positive  (with the appropriate
changes in the direction of the inequality signs) and
you get
(with the appropriate
changes in the direction of the inequality signs) and
you get
- Pr{-1.03*
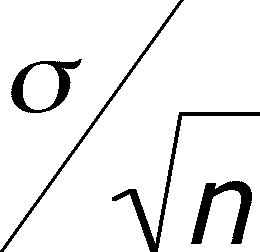 -
-  < -
< -  < 1.03*
< 1.03*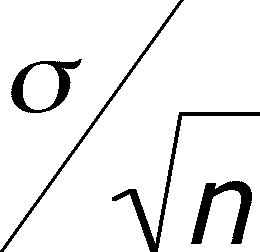 -
-  } = 0.75
} = 0.75
- Pr{
 - 1.03*
- 1.03*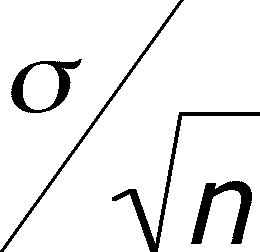 <
<  <
<  + 1.03*
+ 1.03*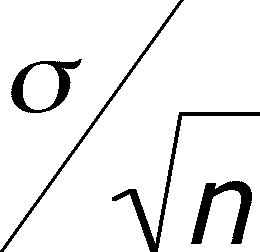 } = 0.75
} = 0.75
- This last expression is a confidence
interval.
- It says that there is a 75% chance of the true
mean being between the sample mean minus a term (based on a z value and the
standard error of sample means) and the sample mean plus the same term.
What if we do not know
the value of the standard deviation of the population?
We have done it, we have found out
where the true mean is with a confidence level of 75% but there
is a fly in the ointment, a bit of unfinished business
- How can we find
 unless we know
unless we know  ?
?
- We need an estimator of
 and we will turn to the same place
as before, the SE of the mean (which was discussed above)
and we will turn to the same place
as before, the SE of the mean (which was discussed above)
- There is a second problem, because the normal was
calculated with
 , not with SE or S
, not with SE or S
- It turns out that the
distribution of means follows a curve called Student's
t, which is similar to the normal
- it
is symmetric with a single mode, just like the normal
- it
has a larger standard deviation term than does the normal
- the difference between the
t distribution and the normal is dependent on the sample
size, such that smaller sample sized are less like the
normal and larger are more similar
- when sample size is
infinitely large, the t and the normal distributions are
identical
Calculating
a confidence interval using the t-distribution
We can re-write the last equation
for a confidence interval now
Pr{ -t0.75*SEx
¾
-t0.75*SEx
¾
 ¾
¾  +t0.75*SEx} = 0.75
+t0.75*SEx} = 0.75
so we need to calculate
 ± t0.75*SEx
± t0.75*SEx
- We know how to do the sample mean and SE (from
above), but what is t?
- t
refers to the student's-t distribution. It is a platykurtic (flattened)
version of the normal distribution. There is more than one student's-t
distribution. In fact, each sample size produces a unique t-distribution.
- The
shape of the distribution changes with n, the sample size. As
n gets larger, the student's-t distribution becomes more and more similar
to the normal (in fact, when n is infinitely large, they are the same.
- In
the figure below, the normal curve is in pink and is the curve with the
highest peak that falls most steeply. Compare it with the student-t
curve for 1 degree of freedom (k is the degrees of freedom, which depends
on the sample size - see below), which is black. The x-axis units are
standard
deviations and the y-axis is probability.
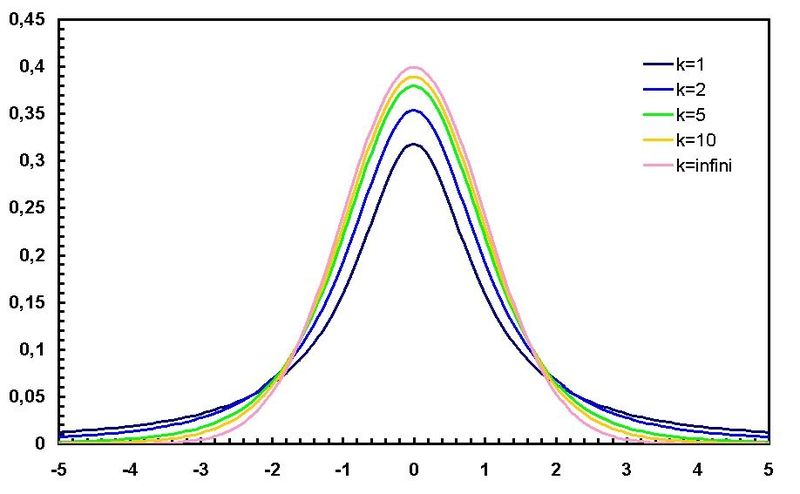
diagram
from Wikipedia, Student's t Distribution entry, used here under GNU license
- The
peak of the student's-t distribution (black) is lower than the normal (pink)
and the tails on either side for the student's t distribution are higher
than for the normal distribution.
- This
means that, if I compare the areas under the curves that are less than
-2 sd, then the area will be larger for the student-t distribution than
for the normal.
- Consider
this: Which curve has more area within ± 1 sd of the mean
(= 0 here). Since there is more area out in the tails for the student's-t
distribution, then there must be less in the center, so it is the
normal with more area (= greater probability) within a standard deviation
of the mean.
- This
makes sense. A sample provides an estimate of the population.
Estimates are not as accurate and so a curve based on estimates should
have more "spread." As the size of the sample increases,
the estimate gets better and better, which happens here because the student's-t
distribution becomes more like the normal is n increases.
- We can look the cumulative areas (probabilities)
up in table 4, where the table body is the upper tail probability of the t-distribution
and the rows an columns depend on the degrees of freedom and the critical
value you want to use
- Degrees of freedom are
n-1 when only one parameter is being estimated (we are trying to estimate
only
 )
)
- The
table lists only the upper tail, and we are concerned about
 being
both too small as well as too large, so we need to divide the area of
the tails (= 1 - confidence level) in half to look it up
being
both too small as well as too large, so we need to divide the area of
the tails (= 1 - confidence level) in half to look it up
- if
you want a confidence of 95%, then (1 - confidence level) = (1 -
0.95) = 0.05 but you have to look up 0.025, not 0.05
How Large a Sample Size
This is an important question to
ask when designing experiments.
- If you will be using statistics
to evaluate the results, then you don't want
- to have too few data points
to show a difference between experimental and controls
- to have more data points
than is necessary to show a difference between
experimental and controls
- The
first instance can be a disaster and the second may be an
inconvenience (doing more than needs to be done) or can mean
that you get fewer experiments done because you are wasting
effort
We will use the formula for the
standard error of the mean to estimate n (see above for this
formula)
- You can't do this without some sort of guessing,
but the guessing should make use of prior knowledge and your expertise.
- Consider
what you want the ± portion of the confidence interval to be (see example
below)
- You are measuring the
concentration of a protein, and you think that the
experimental cells might have as much as 20% more than
the control cells. You will have to set up a series of
flasks in which to rear cells and will measure the
concentration of the protein in each flask. How many
flasks do you need to set up?
- You know that the control
cells produce (from the literature or from previous work)
about 25 picograms per microliter of protein with a
standard deviation of 7 picograms per microliter.
- You want to be 95%
confident that your estimate of the concentrations will
be within 5 picograms per microliter of the true mean
- The 95% is an arbitrary
choice, but it means that you have only a 1 in 20
chance of being wrong
- You
chose the 5 value because you expect the experimental to only
be about
5 microliters above the controls (20% of 25, the known mean). At
this stage, this must be a guess based on the experimenter's experience
or on the results of similar experiments.
- So
you want the ± portion
of the confidence interval to be no larger than 5
- the ± portion
is t0.025*SEx,
- t has the subscript
of 0.025 because you want to be 95% confident, so
the critical value is 5% (1-0.95) and this is
divided in half because the table has only the
upper tail probability (=area under the curve),
and you are concerned about both the upper and
the lower tails (missing by being too large or
too small an estimate)
- from the table, t0.025=~2
(you don't know the degrees of freedom yet,
but look at table 4 in the 0.025 column, and the
values drop to about 2 very quickly, so 2 is a
reasonable estimate)
- So, we can find N now
because we have all the information we need
- 5 = t0.025*SEx,
- 5 = 2 * S, and SEx
= S/sqrt(n)
- 5 = 2 * 7 /sqrt(n)
- sqrt(n) = 14/5 = 2.8
- n = 2.8^2 = 7.84, so
you need about 8 flasks to make an estimate accurate
enough for your purposes
Validity of Confidence Intervals
First, the SEx must be a valid estimate
of 
- The
sample must be chosen from the population in a random manner, such that each
member of the population has an equal chance of being in the sample.
- The
population size (N) must be large when compared with the sample size (n).
- The
observations must be independent
- one observation (x) must not influence the
size of other observations (x's)
- consider the removal of a sample and then
not replacing the sample
- you are measuring an enzyme in the gut
of rats
- you have 5 rats and you take out the
intestine and cut it into six pieces. Enzyme concentration is measured
in each piece of gut
- How many observations do you have? You
have 30 (5 rats times 6 pieces per rat)
- How many independent observations do
you have? You have only 5 because the six from the same rat might all
be influenced by the individual characteristics of the rat, and you are
not interested in that rat per se, but in all rats
The confidence interval is valid if
- the
SEx is valid
- the
population from which the sample is drawn is normally distributed
this condition is strict if you want the
CI to be valid for small sample sizes
this condition can be relaxed if the sample size is large, in which case
the population distribution is of no consequence (remember the central
limit theorem)
Independent Samples and the Difference
Between Means
- We often want to compare two different populations.
- Control versus Experimental
- Male versus Female
- Old versus New
- We do this by drawing random samples from each
population and comparing the samples.
- Populations must not overlap, so that the samples
drawn are INDEPENDENT of one another.
- Any population parameters may be compared, but
we will, once again, concentrate on the mean as the best way to compare populations
(this is not always true).
- To
do this, we will speak about a composite statistic (or parameter),
called the DIFFERENCE BETWEEN
MEANS
(the subscrips 1
and 2 are used to identify the different populations or samples)
- For populations this is:
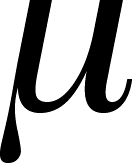 1 -
1 - 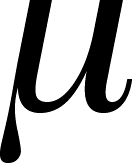 2
2
- For samples this is:
 1 -
1 -  2
2
Standard Error of the Difference Between Means
We will use the standard error of the mean, SExbar,
to get the Standard Error of the difference
between means (= SE(x1 -
x2))
- There are two ways to approach this.
- One pools the variance of each sample to get
an overall variance and then calculates the standard error from this pooled
variance
- The second is called the unpooled SE and it
uses SE from both samples
- If the 2 sample standard deviations are
equal or if the sample sizes are equal, then the pooled and unpooled
SE's are equal
- When the sample sizes are unequal, then we must
choose which to use
- If the standard deviations of the POPULATIONS
are EQUAL, then the pooled is the correct
choice
- However,
the unpooled will be close to the pooled SE
- If the standard deviations of the POPULATIONS
are UNEQUAL, then the unpooled is the
correct choice
- The book recommends that the unpooled be the
only choice, because:
- the
potential problems caused by choosing the unpooled when the
pooled is the correct choice are small because the
unpooled estimate and pooled estimates are usually about
the same size in this case
- the potential problems caused by choosing
the pooled when the unpooled is correct choice can be very serious, leading
to false conclusions
- So we will only work with the unpooled SE (the
pooled SE formula is in the book)
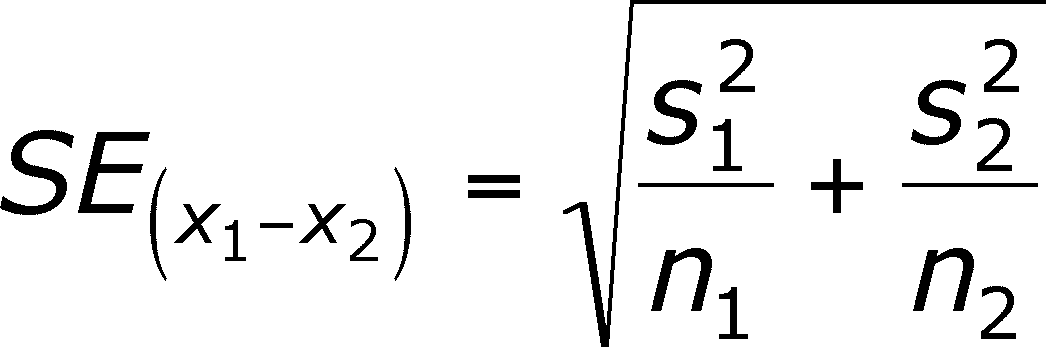
or
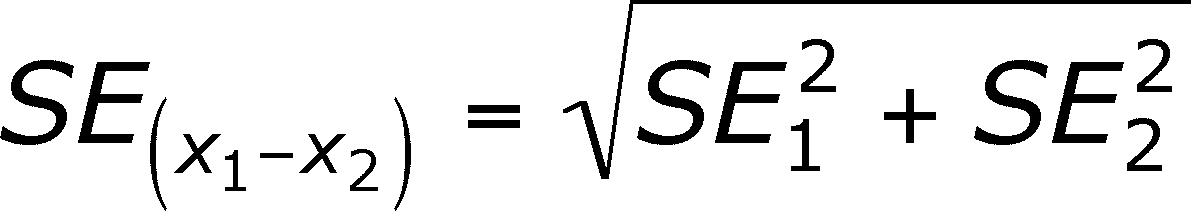
This second form is the same as the first if you
substitute for SE using the definition of SE in the previous chapter.
Confidence Interval for the Difference Between Means
Once you have calculated the standard error of
the difference, this is just an adaptation of the CI formula above:
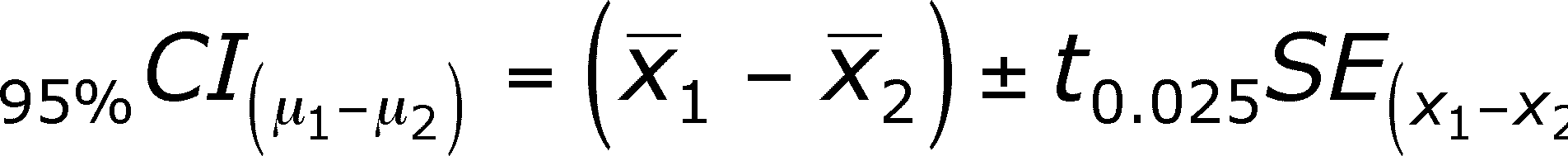
- Notice that I have chosen 95% as the confidence
level. It can be something else, but then the t-value would have to be
adjusted
- Notice also that the CI is for the difference
between parameters (population means) and is calculated from sample statistics
In order to look up the right t value, you need
to know the degrees of freedom, which represents a bit of
calculating:
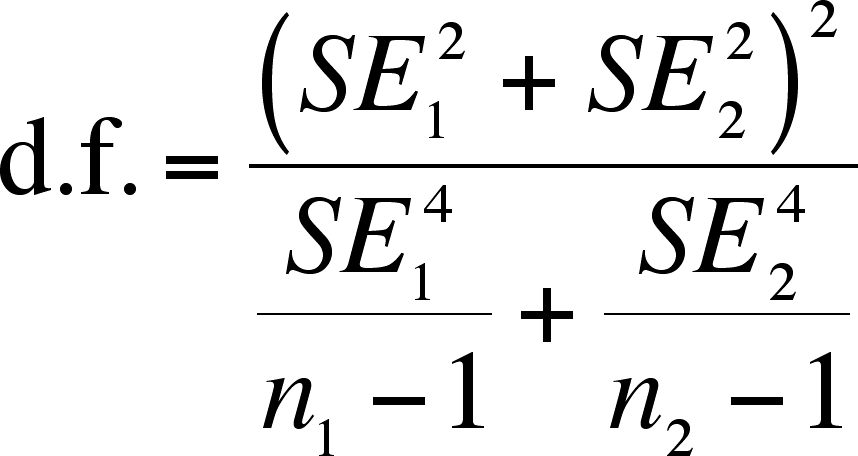
SE1 and SE2 are the sample
errors (the sample standard deviation divided by the square root of the
sample size)
- This
formula = n1+n2-2 if SE1 =
SE2 and
n1 =
n2 and approaches nmin - 1, where nmin is the smaller
of n1 and n2, as sample sizes
and standard errors become less and less equal
- The formula above is the most accurate means
of determining the degrees of freedom. However, you could use either
n1+n2-2 or
nmin - 1 as long
as you are aware of the cost
- n1+n2-2 gives
a confidence interval somewhat smaller than it should be if the SE's and
n's are not equal
- nmin -
1 gives
a confidence interval somewhat larger than it should be unless the SE's or
the n's differ greatly
This test is valid when:
- each
sample is a random sample of independent observations
- the
populations are normally distributed if small populations (relaxed assumption
for large populations due to Central Limit Theorem)
Last
updated October 5, 2011
is a square root also)
![]()

![]() and
and ![]() in it, and we want to know how one relates to the other)
in it, and we want to know how one relates to the other)< 1.03} = 0.75
![]() should lie
should lie -t0.75*SEx ¾
¾
+t0.75*SEx} = 0.75
± t0.75*SEx
![]()
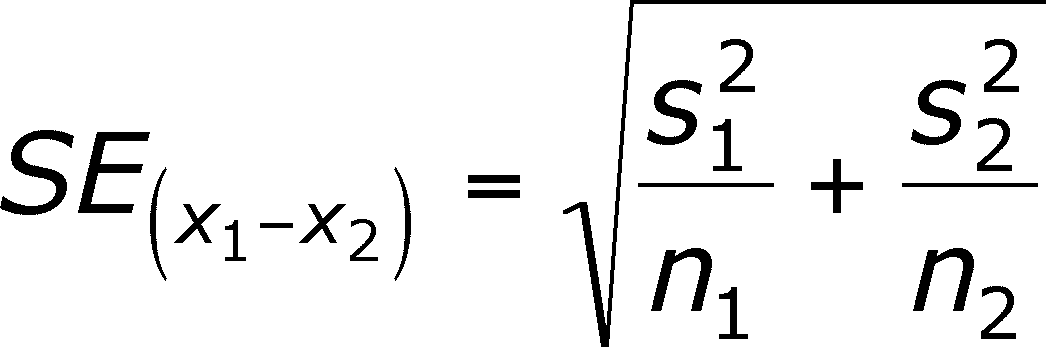
![]()
![]()