 |
BIOL 3110
Biostatistics
Phil Ganter
302 Harned Hall
963-5782 |
| Canis Bay Lake in Canada's Algonquin National Park |
Comparing Two Independent Samples
4th edition Chapter
7
3rd edition
- Chapter 7 (except first three sections on confidence intervals) and Chapter
8 (sections)
Email me
Back to:
Unit
Organization:
Problems:
Problems for
homework
- 3rd edition: 7.23,
7.30, 7.42, 7.44, 8.2,
8.3, 8.8, 7.47,
7.51, 7.57, 7.64, 7.79, 7.82, 7.89, 7.96, 7.97
- 4th edition:
7.2.1, 7.2.8, 7.3.4, 7.3.6, 7.4.2,
7.4.3, 1.2.1, 7.5.2,
7.5.6, 7.6.1, 7.7.1, 7.10.3, 7.10.6, 7.S.5, 7.S.12, 7.S.13
Suggested Problems
- 3rd edition: 7.24,
7.27, 7.38, 7.46, 7.50, 7.54, 7.60, 7.66, 7.68,
7.83, 7.104
- 4th edition:
7.2.2, 7.2.5, 7.2.17, 7.5.1, 7.5.5, 7.5.10,
7.6.4, 7.7.3, 7.7.5, 7.10.7, 7.S.20
Experiments
EXPERIMENTS are studies where the investigator determines
some or all of the important conditions affecting the outcome.
- EXPERIMENTAL UNITS are
the people, things, or situations studied in an experiment.
- TREATMENT is
an explanatory variable that is manipulated by the experimenter. There
may be more than one in an experiment. Treatment variable is another name
for an explanatory variable. It is the hypothesized cause for the effect
measured by the response variable.
- TREATMENT LEVEL is
one of the quantities or qualities of the treatment to which the experimental
units are exposed. There may be as few as two (never just one if one
considers no manipulation as one of the levels, see below).
- CONTROL is the treatment level that represents no
manipulation. It is designed to measure or detect the
outcome if no manipulation of the explanatory variable were
done. It is often the zero treatment
level.
- NEGATIVE CONTROL is a control for the absence of a change in the
response variable when no manipulation is done. For instance, if PCR
is used to produce DNA when the template is added, there is a chance
that other DNA may contaminate the procedure and produce a band even
when the proper template is not there. A negative control would be
a tube to which everything was done EXCEPT THE ADDITION OF THE TEMPLATE.
It should produce no band in the subsequent gel.
- POSITIVE
CONTROL is a control for the ability of the response variable
to change when a known manipulation is done. If the
response depends on the detection of something (presence of a protein
on a gel, release
of light, etc.) then a positive control checks for
the response when the experimenter adds protein to the procedure
or induces light. For
instance, running DNA size markers in one or more lanes
will serve as a positive control that the gel worked and that DNA
should have
separated by size in the experimental lanes. Another
example can be described for the PCR experiment above, in which
the template
you
are searching
for is added to one
tube to be sure that, if the right template is found
in an experimental unit, it will be amplified and appear on the
gel as a band.
- PLACEBO is a special control found in some experiments
with people as the experimental units and it illustrates the subtlety
of designing the right controls. Humans expect to get better when given
a treatment or a pill. They may subsequently report recovery or actually
experience recovery simply from that expectation, no matter whether
or not the pill represents a non-zero treatment level. Thus, to control
for the pill effect, pills had to be given to all in order to detect
the effect of the treatment. However, this is just another example
of a control.
- HISTORICAL CONTROL is a control that is completed before the experimental
manipulations are done. This often is necessary if one is treating
people as not treating someone is not ethical, so those not treated
are those who had the illness before the new treatment was available.
- There is a second flavor of historical
control that is part of a Natural Experiment, which are explained in your ecology class
- BIAS is variation that is the result of a lack of
randomness or independence. Many psychology experiments have been done
from universities with an over-abundance of students as subjects. This
may not represent a truly random sample of any population except university
students and that is probably not the population the researcher intended
to investigate, so this may represent a bias. One might say that the tendency
for people to react to a pill by feeling better is a bias. PANEL BIAS is a bias that results from the altered behavior
of the people in an experiment. Once you tell them they are in an experiment
and something of the rationale and expected outcomes, they may alter their
behavior simply as a result of this knowledge.
- Working with humans presents special problems,
both practical and ethical.
- The practical problems are our focus of interest.
- Humans can perceive the design of an experiment
and may alter their response in light of that perception
- BLINDING is
a fix for this problem that involves not allowing the experimental unit
(the person) to know about which level of the explanatory variable (or
variables) they are experiencing.
- The person who gathers the data may also affect
the outcome of an experiment unfairly (even if unconsciously)
- DOUBLE BLINDING
is a fix for this problem that involves keeping both
the subject of the experiment and those who gather the data from knowing
about which level of the explanatory variable applies to a particular
observation.
Observational
Studies
Data
is gathered by a researcher by observing a situation that would occur without
the researcher's presence or effort in an OBSERVATIONAL STUDY.
- Statistical
tests, like the t-test, are used here to detect differences among groups
of observations, just as in experiments.
- OBSERVATIONAL
UNITS are the persons, things
or situations that are observed.
- VARIABLES are
conditions that can take on more than one value during the experiment.
Variation can be qualitative or quantitative.
- A RESPONSE VARIABLE is the quantity or quality of interest that should
change during the period of observation. There is often one but there
may be more than one response variable in an observational study.
- EXPLANATORY
VARIABLES are the quantities or qualities that are measured
by the observer to explain the changes in the response variable.
- EXTRANEOUS
VARIABLES are the quantities or qualities that are not measured
by the observer but effect changes in the response variable.
Problems with Observational
studies
- Nonrandom
selection of observations (sometimes non-independent)
- Uncontrolled
extraneous variables
- These
problems make it difficult to determine cause and effect relationships
in observational studies
- We
usually say that outcomes are ASSOCIATED,
rather than one causes the other.
- By
observing, we can not tell when one thing causes another or if the
purported cause simply precede the effect, even if it seems logical
based on current beliefs.
- SPURIOUS
ASSOCIATION
- Both
cause and effect can be the effects of a third factor.
- If
A and B occur, with A preceding B, does A cause B (if A, then B)?
- No
if C causes A and then C causes B (if C, then A and then B.
- C0NFOUNDING
- Confounding
occurs when explanatory or extraneous variables are
not independent of one another.
- Example
from my work.
- Yeast
communities are found in cacti from Ontario, Canada to Patagonia
in Argentina.
- Yeast
communities are found in many different species of cacti.
- Data
exists from collections taken from many locales and many species
of cacti.
- Can
we separate the effects that distance has on yeast communities
from that different species of cacti have?
- No,
for the most part. Many locations have only one species of
cactus, so we can not tell if the differences found there are
due to differences cause by different host plants or because
the community is isolated by distance from other yeast communities.
- Thus,
in these studies, host species and collection locale are Confounded.
- We
use the observational approach when the experiment is difficult, costly
or impossible to perform.
- CASE-CONTROL
STUDIES
- Case-control
studies match up similar situations (each cases is an observational unit)
for comparisons, so that extraneous variables have less effect on the outcome.
Importance of Randomizing
We have discussed random allocation previously,
but the importance of this is re-emphasized here.
The reason to do this is to eliminate bias in the
match of experimental units to treatments. This is most effectively done
in a COMPLETELY RANDOMIZED DESIGN in
which experimental units are assigned to a treatment level
randomly, such that each unit has an equal chance of ending up in any of
the groups
This mean that there may not be equal numbers of
units assigned to each treatment level.
An acceptable departure from this is to randomly
assign equal numbers of the pool of experimental units to each treatment
level. Some statistical tests require or work better with if all groups have
the same number of units in them.
Haphazard is not Random
Much bias is not conscious, so just by not
thinking about which to choose does not eliminate bias.
If you are choosing cattle for feeding experiments
by going to the edge of the herd and grabbing the first cow you come to
each time you choose, you are assuming that the cows are located in the
herd randomly. If smaller, weaker cows are pushed to the edge, then you
are picking them first and whichever treatment level is getting filled
first will be filled with the smaller, weaker cows.
Hypothesis Testing with the t-Test
What if you wanted to compare two
means, say a control and an experimental sample mean in order to
find out whether or not they were different?
- You could calculate the CI for
the difference between control and experimental means
- If the CI included 0, then
you might say that you are 95% confident (or 99% or 90%)
that there is no difference between the control and
experimental means
- If the CI did not include
0, then you might conclude that you are 95% confident
that there is a difference between the control and
experimental means.
- There is another, more formal way
of doing this called HYPOTHESIS TESTING
- The case in which there is no
difference between means is called the NULL
HYPOTHESIS
and it is written:
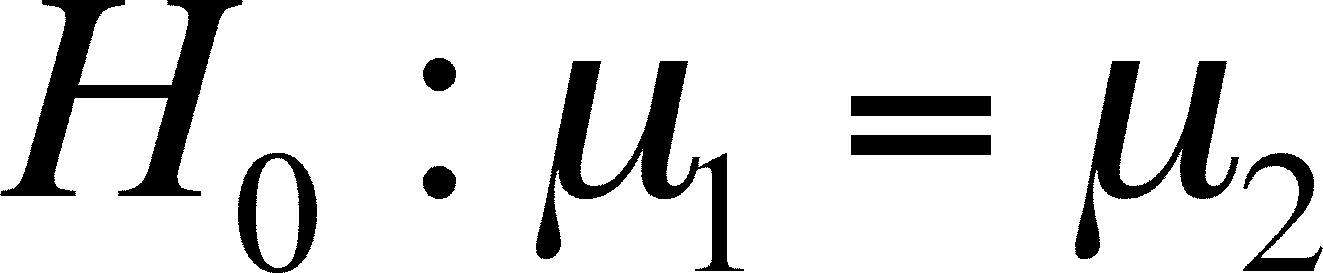
- The case in which there is a
difference between means is called the ALTERNATIVE
HYPOTHESIS
and it is written:
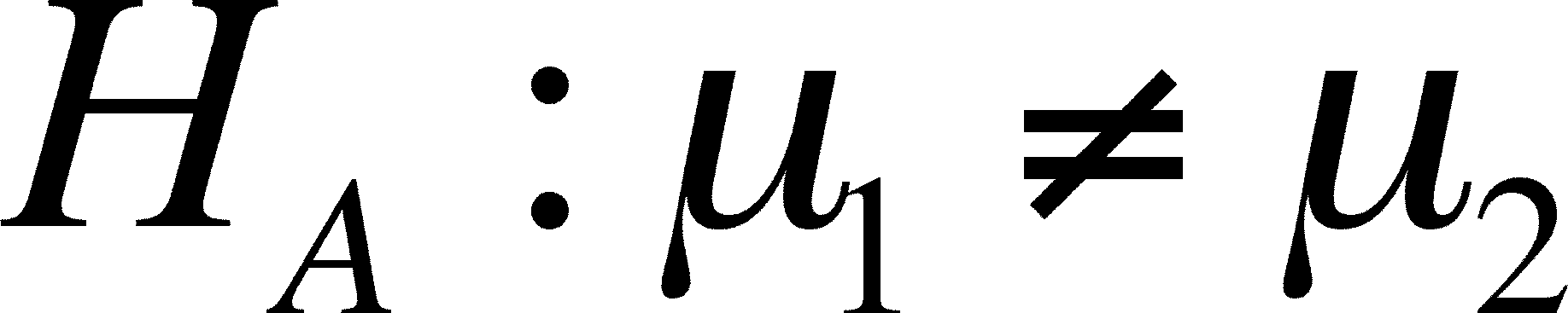
- Note that the experimental can
be larger or smaller than the control unless we specify
otherwise, as we do below.
- You
must make a decision about which hypothesis is correct and we do this by
deciding whether or not to reject the null the null hypothesis.
- If
you reject the null, you
automatically accept the alternative.
- If
you accept the null, you automatically reject the alternative.
- Why do we test the null and not the
alternative?
- The distribution of the difference
between the means (our test statistic) is due to random chance alone
if we assume the null is correct
- We know what to expect if the null
is correct because the t-distribution is based on random chance alone
- If we want to make our decision by
deciding whether or not to reject the alternative hypothesis, we would
need to know the distribution of differences given that the alternative
was true
- This distribution would be based both
on random chance and on the true difference in the means, which we do not
know (we only know the difference between our sample means) and so we don't
know exactly what this distribution actually is
- Therefore, we can't directly test
the alternative and must confine ourselves to testing the null and
using logic to decide about the alternative (if the null is rejected,
the alternative is accepted)
- The
decision about whether or not to reject the null hypothesis is made in three
steps:
- Step
1 -- Decide what the maximum chance of being wrong should be
- This
decision must be made prior to performing the experiment because, if you
make it after, then you can be tempted to change your risk to get the result
you want
- The
maximum acceptable risk of being wrong if you reject the null hypothesis
is called the alpha (
 )-level
)-level
- Step
2 -- Calculate the actual chance of being wrong if you reject the null
by calculating the t-value from
the data.
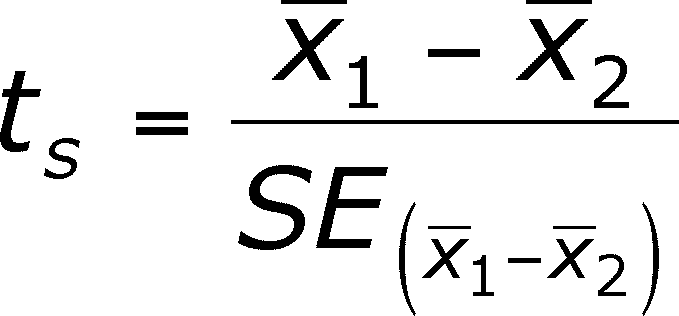
- This is a measure of how many
standard errors apart the two means are, analogous to the
calculation of a z value (remember, analogous, not the equal
of).
- When
testing the difference between two means, the
t-distribution is the distribution of differences one would expect if
the null hypothesis were true (i.e., if the true difference between the
means was zero.
- This
implies that the difference you got between your sample means was due
to random sampling error (given that there is no bias in the data)
- The
t-value describes the probability of the differences one
expects if random sampling error is producing the differences
- Notice
that, by using the t-distribution, you are assuming that the null hypothesis
is true
- Also, by assuming that the null hypothesis
is true, then the expected value of the difference is zero, which is
the mean of the t-distribution
- When
a t-value is calculated, the t-distribution describes how often one
would expect to get a t-value that large or larger
- Larger
t-values are more unusual
- Think
of the shape of the t-distribution - as you go away from the mean there
is less and less area in the tails of the distribution
- So,
what does the area in the tails of the t-distribution represent?
- The
area represents the probability of getting a t-value as large or
larger than the one you got and we call that probability the p-VALUE.
- In terms of deciding about
the null hypothesis, what is the p-value?
- It represents the chance that
the null hypothesis is true, and, by logic, if you reject the null
hypothesis, it is the probability that you are wrong if you reject
(wrong because the null is true and should be accepted)
- Step 3 -- Compare the
 -level
and the p-value (both are probabilities)
-level
and the p-value (both are probabilities)
- If the p-value is smaller than the
 -level
then:
-level
then:
- reject the null hypothesis because
the ACTUAL probability of being wrong (the p-value) is smaller than the
largest acceptable probability of being wrong (the
 -level)
-level)
- If the p-value is smaller than the
 -level
then:
-level
then:
- accept the null hypothesis because
the ACTUAL probability of being wrong is greater than the maximum risk
you will tolerate (the
 level)
level)
- Some things to note.
- There
is no reason to use the same alpha level for all tests.
- If
you want to be conservative and only reject when the difference between
the
means
is
really large, use an alpha level of 0.01 or 0.001 instead of 0.05
- Directional
vs Non-Directional Alternative Hypotheses
- The
p-values listed in the t-table in the textbook are the area of the
upper tail only.
- The alternative hypothesis:
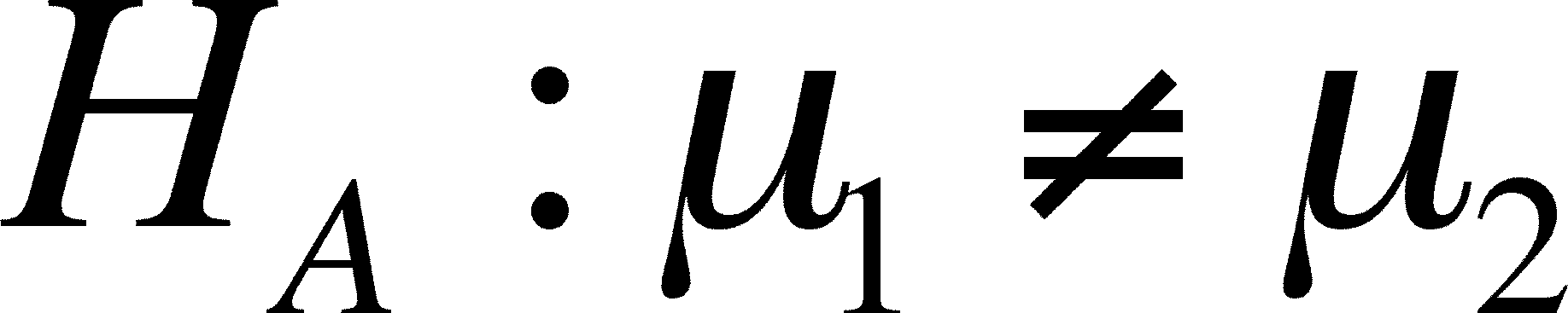
- makes no prediction about which of the means is larger than the
other, just that they are not the same
- This is called a Non-Directional alternative hypothesis
- To get the actual p-value from the t-table
in the textbook when considering whether or not to reject the null
with a non-directional alternative, you must double the
probabilities in the table, as
they are upper
tail
only (where mean 1 is greater than mean 2, so that subtracting mean
2 from mean 1 gives you a positive number)
- The lower tail covers the situation where mean 2 is larger than
mean 1and the difference is negative
- The t table had only values
of the upper tail, so you have to use the column with ONE
HALF OF THE P-VALUE, so that, if the p-value is 0.05,
then you use the 0.025 column (using the 0.05 column
would correspond to a p-value of 0.10).
- Directional alternatives
are discussed below
Conditions
for Validity of the t-test
- These are essentially the same as
for a confidence interval.
- Each sample must be:
- from an independent population
- randomly chosen
- much smaller than the
population from which it is drawn
- Each population must be:
- normally distributed if the
sample size is small
- this is relaxed if the sample
size is large (see the book on the central limit theorem to
find out why)
Error Types and Power
- Above, the idea of error was
introduced. This is not the error we mean by random error, but an
error that lies in drawing a wrong conclusion.
- Thus, if we choose an
 -value
of 0.5, then we are saying that we are willing to go with a 5%
chance of accepting H0 when we should reject it
and accept Ha
-value
of 0.5, then we are saying that we are willing to go with a 5%
chance of accepting H0 when we should reject it
and accept Ha
- There is another type of error
that can be made, and the table below makes the distinction
between the two.
| |
H0 is
true |
H0 is false |
| You accept H0 |
OK |
Type II error |
| You reject H0 |
Type I error |
OK |
- The t-test allows you to choose
the TYPE I ERROR RATE only, which influences the type II error rate
-
 is
the chance of being wrong if you reject H0 and H0 is actually true,
so it is the Type
I error rate
is
the chance of being wrong if you reject H0 and H0 is actually true,
so it is the Type
I error rate
-
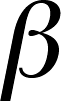 is
the chance of being wrong if you accept H0 and H0 is
actually wrong, so it is the Type
II error rate
is
the chance of being wrong if you accept H0 and H0 is
actually wrong, so it is the Type
II error rate
-
 and
and
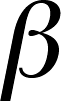 are
dependent on one another, such that decreasing
are
dependent on one another, such that decreasing  ,
the chance of making a Type I error, increases
,
the chance of making a Type I error, increases
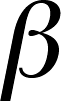 ,
the chance of making a Type II error (and vice versa)
,
the chance of making a Type II error (and vice versa)
- A fictitious example of the difference
between the two types of error
- Two
new home tests for prostate cancer are submitted to the FDA for
approval to
sell them over the counter. Formulation A almost never misses
the presence of the cancer but 80% of the people who test
positive really don't have the cancer. Formulation B has a
much better accuracy in that only 5% of those who test
positive are false positives. However, 5% of the time, the
second formulation fails to detect cancer in patients with
cancer. Which do you approve if you work for the FDA?
- If
you consider having cancer as the null hypothesis and being
cancer free the
alternative, then we can assign the two cases error
types.
- If
the patient has cancer, then H0 is true
and a negative test for cancer means rejecting the
(true)
null hypothesis and accepting the (false)
alternative, Ha. So Formulation
B makes type I errors.
- If
the patient does not have cancer, H0 is
then false. When the test results are positive, you
are
accepting
H0,
although it is false, therefore rejecting
the (true) alternative. This is a type II error.
Formulation A makes type I errors.
- Which
should you, the poor FDA employee, do? In this case, Type I errors
lead to undetected
cases of cancer. Type II error, since it is so common, might
cause a panic of false positives and much extra expense and anxiety.
- Not
sure what to do? Neither am I. Statistics will not solve all your
problems but it might make some problems explicit and get
you to at least consider them.
Directional (= One-Tailed) t-Tests
When you are not interested in the
possibility that mean A is smaller than mean B, only if it is
larger, then you want to use a ONE-WAY t-TEST.
- You first modify the
alternative hypothesis.
- The null hypothesis is
unchanged:
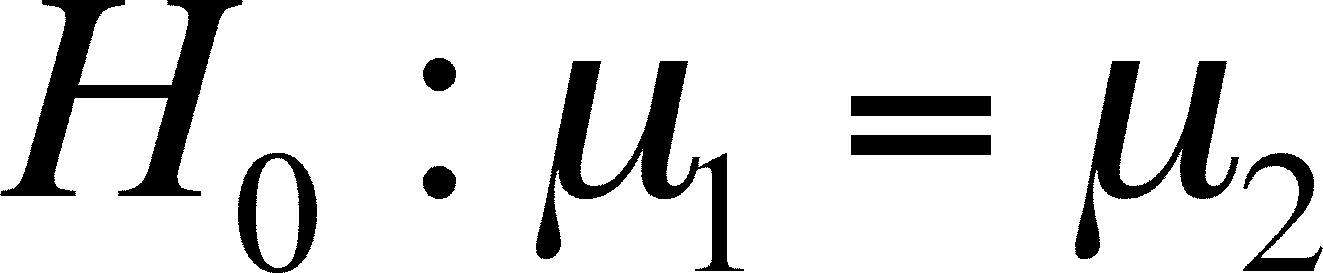
- The alternative is written
one of two ways, depending on which possibility is of
interest:
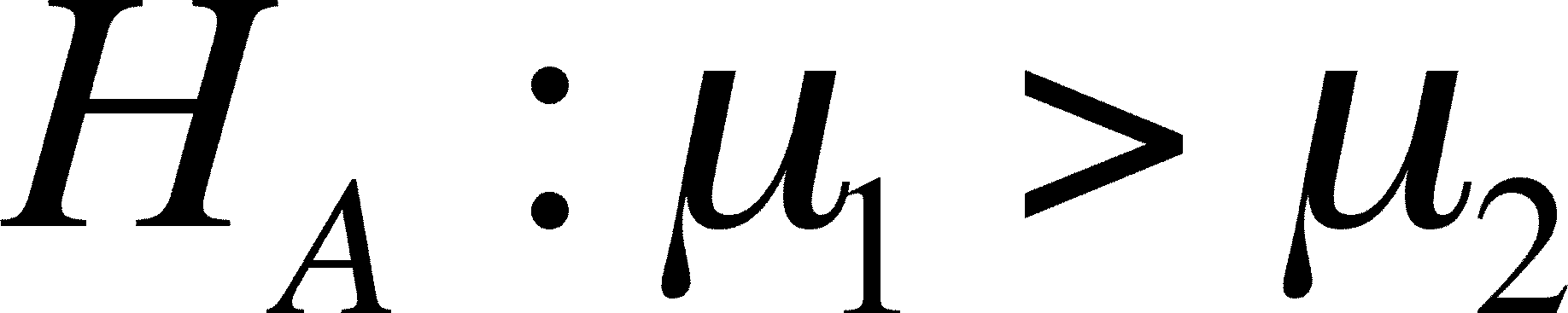 or
or 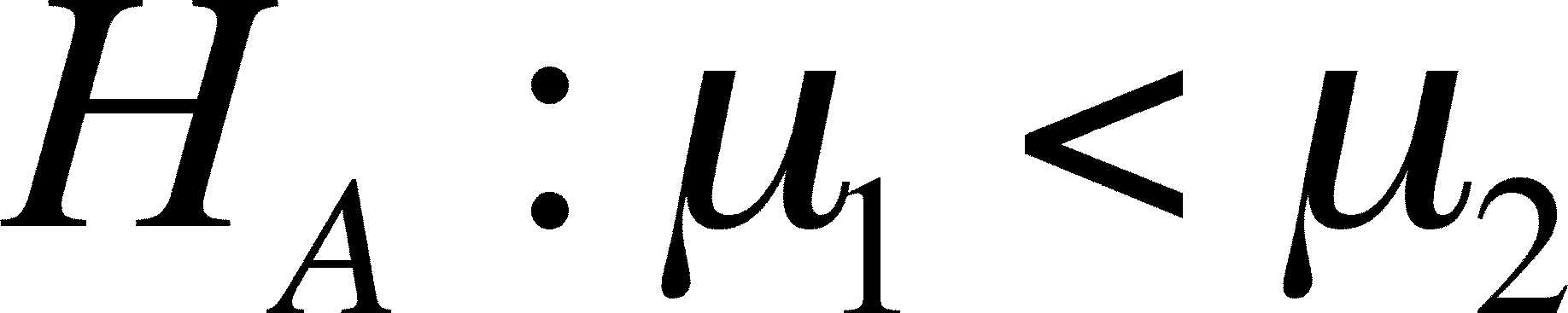
- Once you decide this (and YOU MUST CHOOSE THE APPROPRIATE
ALTERNATIVE HYPOTHESIS BEFORE
PERFORMING ANY ANALYSIS OF THE DATA) you need to alter the t-value you use.
- Before, the area under the
curve that represents the probability of making an error was
found in both tails (to cover error in either direction)
- Now, the error of interest
is only in one direction (depending on Ha), so
all of the area under the curve will be on the
appropriate side
- So,
when using a non-directional alternative, to get a p-value you doubled
the probability found in the textbook's table because the table
lists only the area of one tail and you want both
- Now,
to get a directional p-value, just use the value in the
table, as it is only one tail and you want only one tail
- Remember, that if you choose
the second Ha, your difference between the means
is expected to be negative, and you must put a negative in
front of the t-value because you want the lower tail, not the
upper, and t-values on that side of the mean are negative.
Significance and Effect Size
- After doing a t-test that rejected
H0, what do you conclude?
- In
the scientific literature, we often see the word "significant" used
when describing the results of a statistical test. So, what it
statistical significance?
- When
an author claims that she or he found a "significant" difference
between two means, what is meant is that the chance of the two
means actually being the same (the p-value) is less than the
author's chosen level of "significance", the
 -level
-level
- Statistical
significance does not mean truly significant (by which I mean really
important)
- Importance is a judgment call,
not a mathematically calculated numerical value
- Suppose you weighed undergrads
at MTSU and TSU and recorded these statistics for each sample: MTSU
mean wt. = 145 lbs, s = 13 lbs, n = 1600 (big sample) and for TSU,
mean
wt. = 144 lbs, s = 13, n = 1600 (another big sample)
- The t-value here is 2.18 and
the df = 3198, which results in a p-value = 0.03
- If you had chosen an
 -value
of 0.05, then you would report that there is a significant
difference between MTSU and TSU student weights
-value
of 0.05, then you would report that there is a significant
difference between MTSU and TSU student weights
- Is this important? Only
1 pound? Maybe MTSU students eat a bigger breakfast or wear
heavier shoes. Even if real, is the difference important?
- Your call
- Importance makes reference to the context
in which the data were collected, statistical significance only
refers to the outcome of a statistical test.
- One way of assessing importance
is to calculate and report EFFECT SIZE.
- This is simply the difference
between the means divided by the largest of the two sample
standard deviations.
- In
the case above, effect size is 1 lb/13 lbs = 0.077, so the difference
between the
two is a small fraction of the dispersion of the data
- A
second way is to calculate the confidence interval of the difference
between the means instead of doing the t-test.
- With the confidence interval,
you can may be able to judge the importance of the
difference.
Planning for Adequate Power
- When we pick an -value, we are
picking the chance that we will reject H0 when it is
true, a type I error.
- This means we are minimizing
the probability of reporting a difference between population
means when none actually exists.
- We have seen that a second error
type exists: the error of accepting H0 when it is
false, a type II error.
- This is the error of reporting
no difference between means when one actually exists.
- The ability of a test to reject
H0 when it is false is called the POWER of the test.
- Given that we are comparing two
normally distributed independent populations with equal standard
deviations and we are doing the comparisons by drawing random
samples of equal size, then we can consider the factors that
influence the power of a test.
 -value
-value
- There is an inverse
relationship between and the probability of making a type
II error.
- If you choose to lessen the
type I error rate by using a small
 , it comes at the expense
of increasing the probability of making a type II error.
, it comes at the expense
of increasing the probability of making a type II error.
- If you reduce your chance
of accepting a false H0, then you increase the
chance of rejecting a true H0.

- Larger populations standard
deviations mean that the sample standard deviations are
expected to be larger and so will standard errors of the
mean.
- Larger standard errors of
the mean lead to larger t-test statistics (the
t-statistic denominator is the standard error) and less
chance that you will reject H0, and, thus, a
greater chance of a type II error (=less power).
Difference in means
- Smaller differences between
sample means reduce the power of a test.
- Remember that the
t-statistic is a ratio of the difference between the
means to the standard error.
- If you decrease the size of
the numerator, the ratio will decrease in size, thus
making it harder to reject H0 (= less power)
Sample size
- We have seen that large
standard deviations reduce power because they increase
the size of the standard error.
- Standard errors also depend
on sample size but, because sample size is in the
denominator, larger sample sizes will decrease standard
errors and increase the power of the test.
If you look at these four factors,
you will see that the only one we exert control over is the
sample size.
- (Assuming that we are being as
careful as possible when doing the sampling to minimize error
introduced during the experiment.)
- Planning for power means
choosing a sample size that will produce an acceptable chance
of a type II error.
- To plan you have to:
- Choose an
 .
.
- Know enough to
make a reasonable guess about the population standard
deviations.
- Make an estimate
of the effect size (simplified by the assumption of
equal standard deviations for the populations).
- With these three numbers, you
can look up a recommended sample size in Table 5 in the back
of the book.
- Note that the predicted
trends are there in the table.
- As
 goes down, larger
sample sizes are needed.
goes down, larger
sample sizes are needed.
- As effect size goes up,
smaller sample sizes are needed.
- Also, as power goes up,
larger sample sizes are needed.
Alternative Methods: the Wilcoxson-Mann-Whitney
Test
This test is often used when either
the assumptions of the t-test are not met or when it is
impossible to determine if the assumptions have been satisfied
- It is NONPARAMETRIC
- It tests for a difference
between the samples but not for a difference in a
specific parameter (the t-test is for a difference in the
sample means)
- It is DISTRIBUTION-FREE
- No assumptions are made
about the shape of the distribution of the population or
sample.
- The only assumptions are that
the samples be randomly drawn from independent populations.
The test looks for a difference
between the distributions from two samples.
- It does this by determining the
probability of getting more of the small observations in one
sample than in the other.
- Because only the rank of
the observations are used and not their absolute size, we
say that this test does not use all of the information in
a sample.
- This may mean that it is
less able to detect differences between populations (=
reject H0) than a parametric test like the
t-test, especially when sample sizes are small (see
below).
H0:
There is no difference between the distributions of the two
populations from which the samples have been drawn
The alternative may be either
directional or nondirectional:
non-directional Ha:
The distributions of the two populations from which the
samples have been drawn are different
directional Ha:
The members of population tend to have larger values than
those in population B
The test works by measuring overlap
between the size of sample observations.
- the statistic that measures this is Us
- Method of calculating Us
- Order each sample from smallest
to largest
- Determine K1 and K2
- For each observation in sample
1, count the number of observations in sample 2 that are smaller.
Tied observations count as 1/2. Sum the counts to get K1
- Do the same for the observations
in sample 2 to get K2
- Check to see that there are
no errors by adding K1 and K2. Their total should equal the product
of the two sample sizes. If not, an error has been made
- Us is simply the larger
of the two K values
- The distribution of the critical value can be
looked up in a table at the back of the book (this distribution does not seem
to be in the MSExcel function list).
- Because the K values are discrete, the probability
distribution of Us is not a continuous curve, like the normal,
but a histogram, like the binomial.
- This means that not all probabilities are
possible.
- The
probabilities reported across the top of the table are limits and the
K values below are the largest K value with a probability less than (or,
rarely, equal to) the probability listed at the top of the table
- The discrete nature of the distribution
of Us also means that, when the sample sizes are small, that
there may be no K value with a probability small enough to use a small critical
value (say, 0.01 or so).
- For example, if the probability of the
largest K is 0.15, the you will not be able to reject H0 with
an
 -value of 0.01
-value of 0.01
Conditions for Validity
of the Wilcox-Mann-Whitney Test
Each sample must be:
- randomly
drawn
- from
an independent population
Last updated March 20, 2013


![]()
![]()
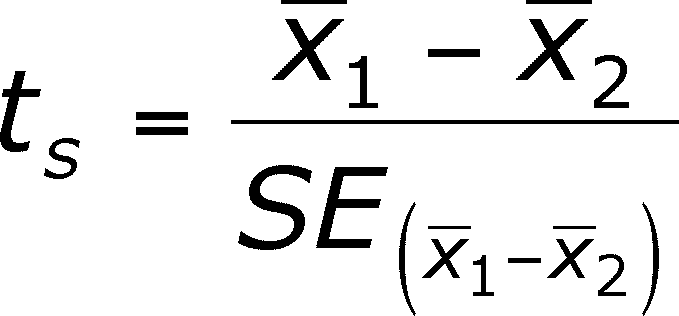
![]()
![]() or
or ![]()
-value
, it comes at the expense of increasing the probability of making a type II error.
.