Handout on Rarefaction Calculation	BIOL 4120 Principles of Ecology
	Harned Hall 301 (615) 963 - 5782
Above: Young Eucalypt trees from Australia growing in Brazil to provide fiber for disposable diapers. The newly planted trees are in the foreground and the dark green band behind them is the forest after only 5 years! Vast fields of eucalypts have replaced the native ecosystem, the Atlantic Forest, one of the most diverse and threatened of all terrestrial ecosystems.

Rarefaction (From Lecture 16)

• Correction for bias in species number due to unequal sample sizes by standardization to the number of species expected in a sample if it had the same total size as the smallest sample
  • very similar to the idea behind Effective Population Size for comparing genetic drift in two populations with different mating systems or different histories
• Say you had two samples, A with 100 individuals total and those 100 individuals distributed among 9 species and sample B with 25 individuals distributed among 4 species.
  • Rarefaction answers the question "How many species would I expect in sample A if I had caught only 25 individuals in all instead of 100?"
• N = total number of individuals in rarefied sample (100 in the sample above)
• N_i = number of individuals in the i^th species
• n = size of the smaller sample (25 in the example above).
• We want to calculate E(S), which is the expected number of species in the sample IF THE SAMPLE WERE OF THE SMALLER SIZE (n).

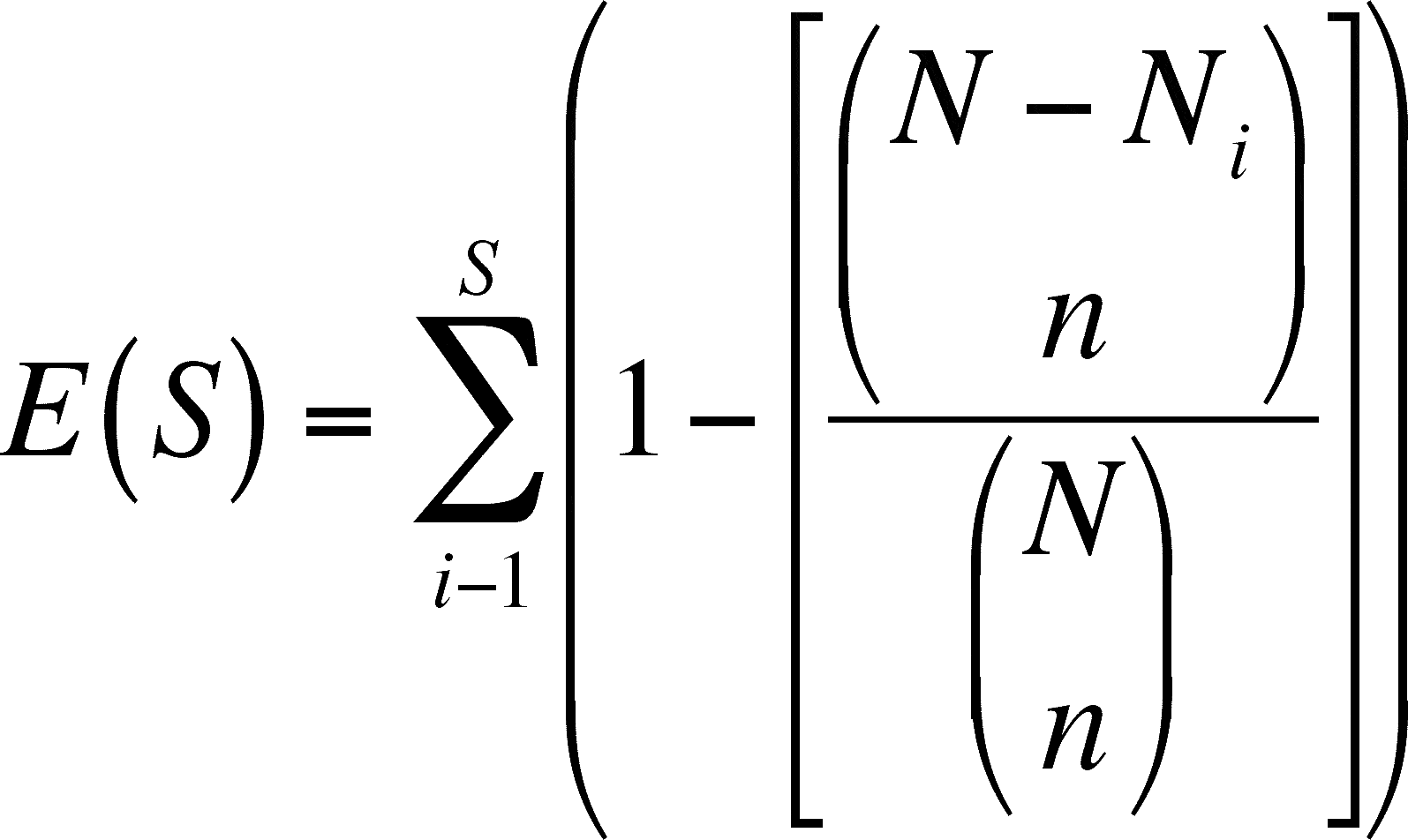
• Look at this expression and simplify it in your mind. Each term that you sum is 1 minus a fraction, so each term you sum is less than 1. You are summing up S (= number of species in the sample) terms, so the sum will have to be less than S (since each term is less than one and there are S terms). Therefore, the expected number of species will be less than the actual number of species
  • This is because you would expect to capture fewer species in a smaller sample.  The rarer species have less of a chance of being taken.
• The expressions within the inner most parentheses are not fractions, they are combinations (note that there is no horizontal bar and see a discussion of combinations in Lecture 13 from BIOL 3110, my biostats class). These combinations are defined as:

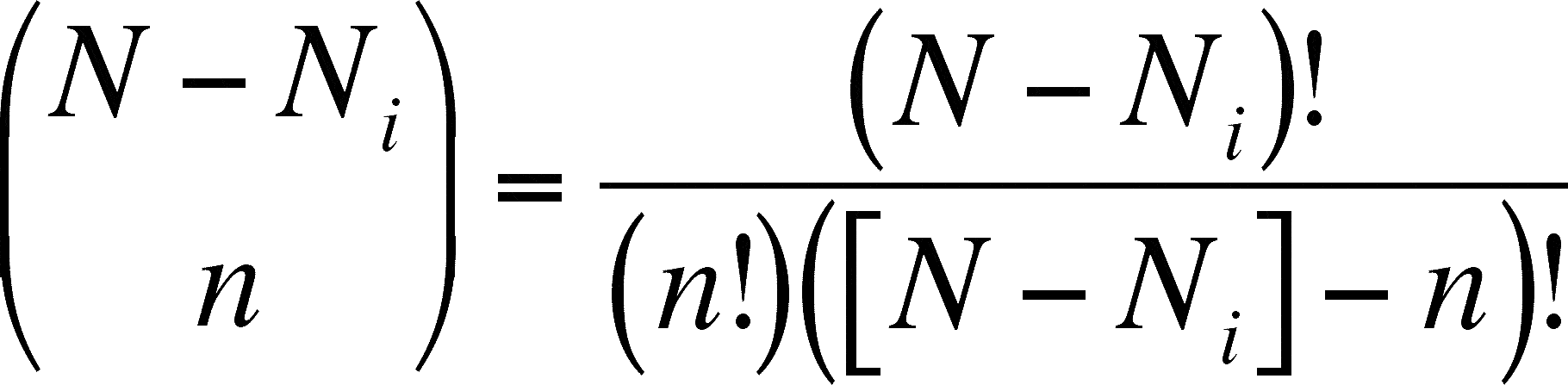
• and

• remember that the fraction on the left of the = sign is not a fraction (note: no horizontal bar), and the fraction on the right is one. The ! means that the expression is a factorial. The expression on the left is called a combination because it gives you the number of ways to take N objects n at a time. For instance, there are three ways (= 3!/2!1!) to group 3 objects 2 at a time (1&2, 1&3, 2&3). Factorials (indicated by !) are gotten by multiplying the number times one less times two less times ...
• What you are calculating in the combinatorial expression found in the numerator of the fraction within the summation in the top equation is the number of combinations one can make (of the same size as the smaller sample size, n) without any of the species of interest present (this is why we use N - N_i and not N_i here).  The total number of combinations possible is calculated by the combinatorial expression in the denominator.  This fraction is then the proportion of combinations (each one represents a possible sample) that contain none of the species of interest (species i).  This can be seen as the probability of not getting that species in the sample and this fraction is subtracted from 1.

Without rarefaction, one can not compare samples that have different number of individuals in each sample

Calculating Rarefaction

Remember that

• N = total sample size
• S = number of species
• n = standard sample size used for comparison
• N_i = number of individuals in the i^th species

  Logically, the sum of the N_i values must be equal to N.

To compare all three lakes, we need to rarefy the samples from Central America and Argentina to the smallest sample, North America

The book does not say, but n must be THE SMALLEST SAMPLE SIZE

The criterion is that N > n, or you will not be able to do the combinatorials when N < n

Therefore, rarefaction always adjusts down, never up.

So, we can only ask "How may species would I have gotten in this sample if it had been as small as the smallest sample?

We will use n = 25 from the North American A sample and rarefy the North American B and Argentine samples

In the Central American lake sample, we do not get much of a correction (too small to show up). Why?

• This sample is very even, and if you reduce the sample size, all four species should be sampled, as all are about equally likely to be sampled

This situation is a bit different for the Argentine sample, where the sample is not so even, although the richness is greater.

Here, there is a noticeable correction. Why?

• The less common species are much more rare than are the most common, and so, they might not be sampled at all in a smaller sample.

The last example rearranges the Argentine data, but keeps the number of species (6) and total sample size the same (106). What it does is make species G more dominant at the expense of all other species (look at the Ni column here and compare with the previous Argentina table).

I included this example for two reasons

• Reason 1 - notice that the effect here is much more drastic because the community is much less even. Now, you expect to get only 4.18 species when you sample only 25 individuals.

• Reason 2 - Suppose that the number of species G was 82 (and there were two less of Species K, to keep the total the same). When you calculate this rarefaction, you run into an impossible situation. The combinatorial in the numerator for species G is impossible to calculate. It is 24 over 25. You can't calculate this, because it becomes

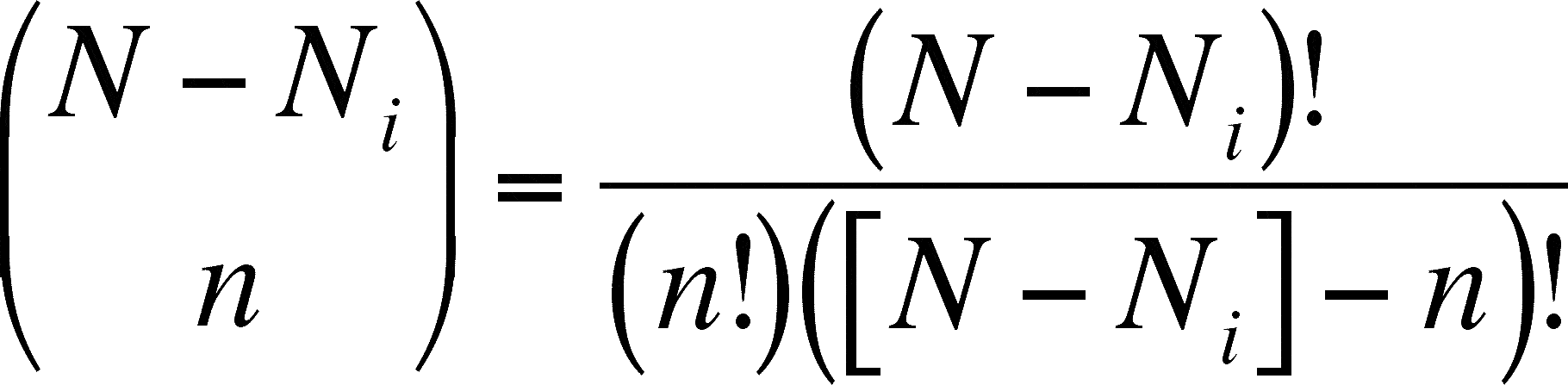
The -1 from the ((N - Ni) - n) factorial (from 24 - 25) is the problem.   You must set this combination to 0 to do the calculations in the rarifaction table because the combination (24 over 25) means you want to calculate the number of combinations of 25 objects one can make with only 24 objects to combine!  Obviously, there are no combinations possible and the answer is 0.  When doing these calculations in a spreadsheet, the program will return some sort of error code for any situation in which you have asked for the factorial of a negative number.  Whenever this occurs, simply set the value of the calculation at 0 and proceed with the calculations.

So, we see that rarefaction is a bit more involved than the text makes out, but still a necessary exercise when making comparisons of species richness among samples that differ in size.

In addition, honesty makes me disclose that this is not the only way to rarefy a sample

For example, one might use a bootstrap approach (made possible by the speed of computers)

In this approach, one subsamples a larger sample repeatedly and then calculates the parameter of interest based on the subsamples

• For the above example comparing the Argentine lake with the North American lake, one would make a subsample by taking the 106 individuals in the larger sample and randomly choosing only 25 of the 106 to be in the subsample.  One would then count the number of species in the subsample and that would be one bootstrap estimate for species richness.

Next, one would resample the original 106 individuals again, choosing another 25 at random (some of those in the second subsample could have been in the first) and recalculate the number of species.

Repeat the subsampling many times (this is why a computer is necessary, 10,000 is a good number of subsamples), each time getting an estimate of the species richness.

Finally, average the 10,000 richness values for the 10,000 subsamples and use that average as your rarefied estimate of richness [ = E(S) in the formula above].

The bootstrapping approach supplies an additional bit of information.  One can do the bootstrap estimate for any subsample size and graph the expected number of species in the sample versus the sample size.  This is a Rarefaction Curve and it usually has a steep portion before it plateaus as the subsample size approaches the larger sample size.  If your smaller sample is in the plateau region, the two samples are reasonable compared.  If not, your smaller sample most probably is deficient as a sample of the diversity (compared with the larger sample).

Last Updated on July 23, 2007